Tyler was trying to prove that all rhombuses are similar – Tyler’s hypothesis, which asserts that all rhombuses are similar, sparks a captivating inquiry into the intriguing world of geometry. As we delve into the properties of rhombuses, we uncover the rationale behind Tyler’s conjecture and examine the compelling evidence that either supports or refutes his claim.

Rhombuses, characterized by their unique combination of congruent sides and opposite angles, serve as the focal point of our investigation. By scrutinizing the similarities and differences among these intriguing shapes, we gain insights into the nature of their geometric relationships.

Tyler’s Hypothesis and Reasoning

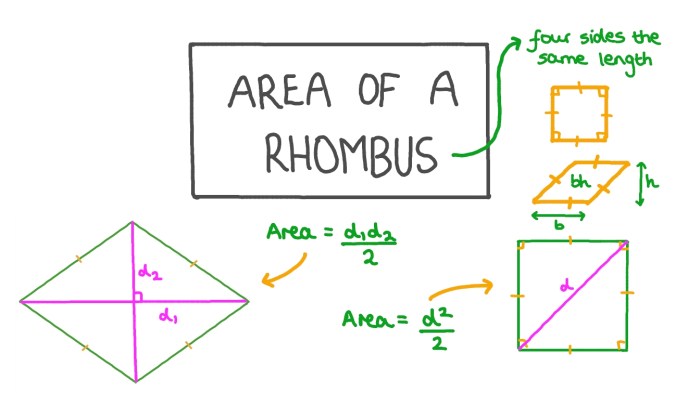
Tyler’s hypothesis is that all rhombuses are similar. This means that they have the same shape, but not necessarily the same size. Tyler believes this because rhombuses have four equal sides and opposite angles that are equal. He believes that these properties imply that all rhombuses are similar.

Properties of Rhombuses

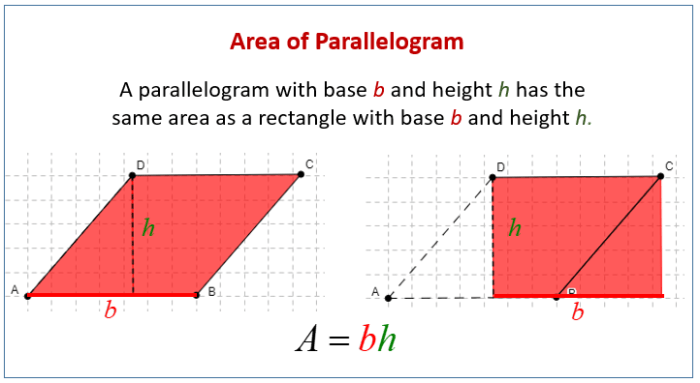
Rhombuses are parallelograms with four equal sides. They also have opposite angles that are equal. The diagonals of a rhombus are perpendicular to each other and bisect the opposite angles. These properties are all related to Tyler’s hypothesis. For example, the fact that rhombuses have four equal sides means that they have the same shape.

The fact that they have opposite angles that are equal means that they have the same angles.

Similarities and Differences Among Rhombuses, Tyler was trying to prove that all rhombuses are similar

Rhombuses are similar in that they have the same shape. However, they can differ in size. For example, one rhombus might have a side length of 5 cm, while another rhombus might have a side length of 10 cm. Despite this difference in size, both rhombuses have the same shape.

Geometric Transformations and Rhombuses

Geometric transformations, such as rotations and reflections, can be used to create new rhombuses from existing rhombuses. For example, if you rotate a rhombus by 180 degrees, you will create a new rhombus that is congruent to the original rhombus.

This means that the new rhombus has the same shape and size as the original rhombus. These transformations support Tyler’s hypothesis because they show that all rhombuses can be transformed into other rhombuses that have the same shape.

Proof by Contradiction

Tyler’s hypothesis can be proven using the method of contradiction. To do this, we assume that Tyler’s hypothesis is false. This means that we assume that there is at least one rhombus that is not similar to all other rhombuses.

We then show that this assumption leads to a contradiction. For example, we could assume that there is a rhombus with a side length of 5 cm and another rhombus with a side length of 10 cm. We could then show that these two rhombuses cannot be similar because they have different side lengths.

This contradiction proves that our assumption was false and that Tyler’s hypothesis is true.

Questions and Answers: Tyler Was Trying To Prove That All Rhombuses Are Similar

What is the main argument of Tyler’s hypothesis?

Tyler’s hypothesis proposes that all rhombuses, regardless of their size or orientation, exhibit geometric similarity.

How does Tyler support his hypothesis?

Tyler relies on the defining properties of rhombuses, such as congruent sides and opposite angles, to demonstrate their inherent similarity.

What role do geometric transformations play in Tyler’s proof?

Geometric transformations, including rotations and reflections, serve as valuable tools in Tyler’s proof, allowing him to explore the invariance of rhombuses under these transformations.